
Control Barrier Functions (CBFs) and Artificial Potential Fields (APFs): How They Compare
In robotics, collision avoidance is a critical feature for any intelligent or autonomous system. There are different ways to implement avoidance algorithms, but this post will highlight two: Control Barrier Functions (CBFs) and Artificial Potential Fields (APFs).
Control Barrier Functions (CBFs) are a core component of 3Laws’s technology. They are central to our understanding of safe behaviors, as they precisely characterize a robotic system’s safety and inform on how they can be kept safe.
This precision is a major differentiator that separates our technology from existing collision avoidance methods in robotics. In this blog post, we outline a direct comparison between CBFs and potential fields, one of the most common obstacle avoidance algorithms. [And for the full technical paper on all of this, head here!)
A Short History of Collision Avoidance Methods
Artificial potential fields (APFs) and their variants have been a staple for collision avoidance of mobile robots and manipulators for almost 40 years. Its model-independent nature, ease of implementation, and real-time performance have played a large role in its continued success over the years. They were first in the seminal paper by Oussama Khatib in 1985, and they’ve seen continual use and development ever since.
Control barrier functions (CBFs), on the other hand, are a more recent development, commonly used to guarantee safety for nonlinear systems in real-time in the form of a filter on a nominal controller. First introduced by Aaron Ames in 2014, they have seen a quick rise in usage in academia. In contrast to APFs, CBFs are implemented as a convex optimization problem, requiring significantly more computational power than APFs, however still practical for lightweight, low-power embedded systems.
Use in Academia and Industry
While control barrier functions are being rapidly adopted by the academic community, they are still referenced less heavily than artificial potential fields. Searching Google Scholar for [“control barrier function” OR “control barrier functions”] returns 1,710 results in the past year, while [“artificial potential field” OR “artificial potential fields”] returns 4,740.
Moreover, their use in industry is less common, as results in academia tend to take 10-20 years to see widespread use in industry. For example, Model Predictive Control (MPC) has been around since 1970, and has only in the last decade seen widespread use in industry.
How They Work: A Simple Example
The figure below showcases a simple 2D robot moving around obstacles with both methods.
APFs:
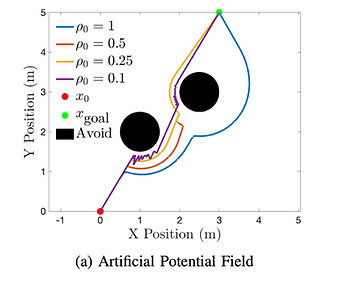
An artificial potential field works like it sounds. A vector field is created by the combination of an attractive force towards a goal location and a repulsive force resonating from the obstacles. The result is a force that pulls you towards a goal while pushing you away from obstacles along the way.
As you may expect, it can be very difficult to tune a potential field to work well in a variety of environments. With potential fields, as showcased below, the performance of the system is highly dependent on the parameter \rho_0, which parametrizes the repulsive force given off from obstacles.. When it is too small, the path is oscillatory, and when it is too large, the path becomes inefficient. At a value of \rho_0 = 0.25, the robot even gets stuck between the obstacles.
CBFs:
In contrast, a control barrier function has no notion of attractive and repulsive forces. Instead, a CBF is a constraint on the system to avoid undesired behavior, like running into an obstacle. It is paired with a nominal controller that tries to achieve the desired tasks, but not necessarily in a safe manner.
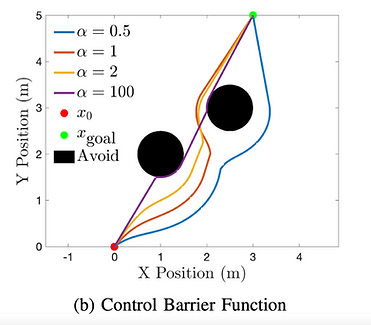
In this example, the nominal controller is the same vector field as the APF, but without the repulsive forces. It is simply the gradient along the path to the goal point.
As seen below, one of the premier advantages in CBF implementations is its performance in a wide variety of parameter ranges. The performance is very consistent among a wide range of values for the sole tuning parameter, \alpha, which determines how quickly the robot is allowed to approach the obstacles.
Quadrotor Example
In a real-world setting, with more complicated robots, the tuning issue becomes even more severe for heuristic-based methods. Striking the right balance between conservative behaviors and oscillating results is difficult, especially in the transition from simulation to hardware. You can see how much more oscillatory the results are for the potential field than the CBF implementation below:

The results for the control barrier function, which was untuned with a default parameter value of \alpha = 1, faced no issues with oscillations and was easily able to make it through tight gaps in the obstacles.
The Core Advantage of Control Barrier Functions: Provable Safety
While we showed in the above examples that CBFs outperformed APFs, many would argue that well-tuned APFs would achieve similar levels of performance or better. The core advantage that CBFs have, however, is in their rigor.
A control barrier function can be used to generate a mathematical guarantee of safety, in a way that APFs cannot. A system operating under a control law defined by a CBF can be proven to stay within a predefined set of states, in a way that APFs cannot.
How 3Laws is Utilizing Control Barrier Functions
The provable aspect of CBFs is central to 3Laws’s approach to safety. With properly generated and implemented CBFs, we can certify that a system will stay safe under certain assumptions on the integrity of various system components like sensors and actuators. 3Laws is expanding the scope of these certificates to handle more and more system faults and failures.
We see CBFs as a way to generalize safety of robotic systems at the behavior level. Currently, regulations are relatively disjoint between the different industries of robotics. Our goal is to simplify and unify how safety is managed and certified, to simplify the process for developers and ensure a safer tomorrow!