The (Not So) Simple Math Behind Redundant Systems

Control systems are designed to be reliable, but failures can and do occur. One of the most effective ways to mitigate these failures and ensure consistent operation is through redundancy. By incorporating backup components or subsystems, we aim to bolster the system’s resilience against unexpected issues. In this discussion, we’ll explore the concept of redundancy, its role in enhancing system reliability, and the complexities associated with the application of redundant systems.

The Important of Redundancy

Redundancy refers to the inclusion of backup components or subsystems that can take over the control functions in the event of a failure in the primary components or subsystems. The primary goal of redundancy in control systems is to enhance system reliability and fault tolerance. In redundant systems, redundancy is used to ensure that a system continues to operate or can be safely shut down in a controlled manner even when one or more components fail.

Let’s say we want a redundant power supply to ensure a steady supply of power in the event of component failure. We have two power supplies, PA and PB. To build a redundant system, we require a third component, C, that monitors the status of the two power supplies and controls their operation.

In normal operating conditions, both PA and PB are active and share the load. The control unit continuously monitors the status of both power supplies to ensure they are working correctly. If the control unit detects a failure in PA, such as an electrical fault or a loss of output voltage, it triggers an alarm and takes appropriate action. This action may include disconnecting PA from the load.

After detecting the failure of PA, the control unit switches the load over to PB. This transition can happen automatically and quickly, ensuring uninterrupted power to the system. PSU A can be safely isolated for maintenance or replacement. Meanwhile, PB continues to power the system. Once PA is repaired or replaced and verified to be functioning correctly, it can be brought back online, and the control unit may switch the load back to both PA and PB for normal operation.

Calculating Reliability

In order to calculate the reliability of a system, we need to first understand how additional components affect reliability.

In robotic systems, we often have subsystems that rely on one another. In this case, you can consider them to be in series, as shown below.

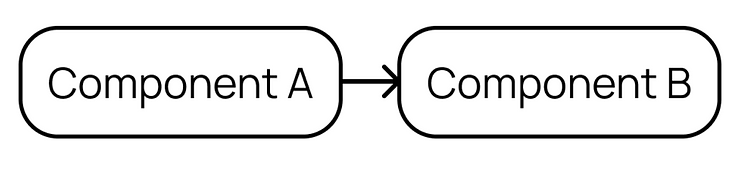
In this case, The reliability is calculated as RA*RB. Therefore, the probability of failure is equal to 1-(RA*RB) = 2%.

If two components are instead redundant, i.e. each can fulfill the task independently, we can consider them to be in parallel, as shown below.

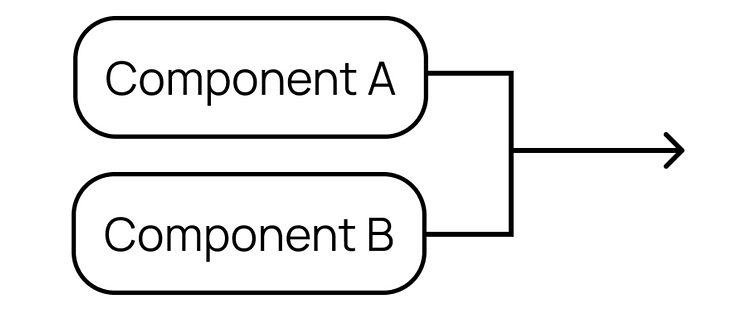
In this case, the reliability is calculated to be 1-((1-RA)*(1-RB)), where RA is the reliability of component A and, therefore, (1-RA) is the probability of failure of component A. If the probability of failure of each component is 1%, then the probability of simultaneous failure for both components is 0.01%.

It is clear that redundancy has a huge effect on the failure probability of a system. Unfortunately, the math is not quite that simple in practice. As demonstrated in the example, we at least need an additional component to monitor for failures and control the system. From the example, we have

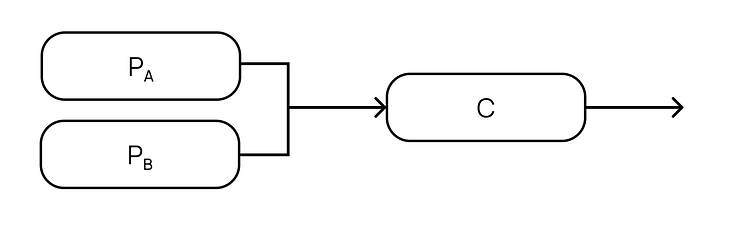
Using the same failure probability of 1% for the power supplies and controller, we can compute the reliability of this system to be (1-((1-PA)*(1-PB)))*C which is equal to 0.9899, or a failure probability of 1.01%. Compared to the probability of failure of just the two power supplies, which is 0.01%, this is two orders of magnitude higher. Typically, component C would have much higher reliability than components PA and PB, so this result would not be as exaggerated.

Further Considerations that Complicate Reliability

However, again, we have made more assumptions to arrive at this reliability. This approach assumes that the controller’s failure is not directly related to the power supply failures. If the controller’s failure is dependent on the power supplies, the analysis becomes more complex, and you may need to consider fault trees and conditional probabilities in your calculations. The specific approach to reliability analysis may vary depending on the exact details of the system and its failure modes.

This approach also assumes that PA and PB are fully independent. In the context of robotic systems, this would mean that each component would need both hardware and software redundancy, Hardware redundancy involves duplicating critical hardware components such as sensors, actuators, controllers, or even entire subsystems. If one component fails, the redundant component can take over, ensuring that the system remains operational.

In the design of redundant systems, software redundancy ensures the control system has multiple software components that perform the same functions. If one software component encounters a failure, the redundant software component can take over to maintain system operation. Dissimilar software is desirable to avoid common-mode failures. This typically requires multiple teams working separately on development without the use of shared libraries. While these strict development requirements can reduce the reliability of each individual software component, the gain from the redundancy very quickly increases the reliability at the system level.

Redundant Systems are a Must

Redundancy is essential in critical control systems, such as those used in aerospace, automotive, industrial automation, and safety-critical applications. It helps prevent catastrophic failures, improves system availability, and enhances overall system reliability.

However, redundancy comes with added complexity and cost, so it’s typically implemented based on the specific requirements and risk assessment for a given application. Moreover, it is not a simple value to compute. Decisions to incorporate redundancy should be grounded in a thorough evaluation of specific requirements and a comprehensive risk assessment for each application.