
Data-Driven System Identification: Mixing Classical and Modern Approaches
Data-driven system identification for robotic systems refers to the process of determining a system’s dynamic model based on observed data. Instead of relying solely on physics-based modeling, which can be complex and sometimes lacking in precision, data-driven approaches use experimental data to identify the dynamics of the system.
At a high level, data-driven system identification is a process of deriving mathematical models or representations of a system’s behavior and dynamics using real-world data collected from the system’s operations. It involves analyzing the data to extract relevant patterns, relationships, and underlying structures, which are then used to construct a model that accurately describes how the system behaves.
However, there are different ways to implement data-driven system identification. At the one end, there is a dynamics-based (or physics-based) approach – and at the other, there is a pure data-driven approach, or “black-box,” approach. In this blog, we outline the advantages and disadvantages of data-driven system identification – and outline why a hybrid approach can be used to achieve the best results.

Advantages of Data-Driven System Identification
Instead of relying solely on physics-based modeling, which can be complex and sometimes lacking in precision, data-driven system identification uses experimental data to identify the dynamics of the system. Here are some advantages of this approach for robotic systems:
- Model Precision – Data-driven identification can often provide more accurate models, especially when the physics-based models are complex or hard to derive.
- Compensating for Uncertainties – Physical robotic systems always have some form of uncertainties, be it from manufacturing variances, wear and tear, or unmodeled dynamics. Data-driven approaches can help identify and compensate for these uncertainties.
- Reduction of Modeling Effort – For complex robots with many interacting parts or those that operate in complex environments, deriving a physics-based model can be exceptionally challenging. Data-driven methods can help alleviate this modeling effort.
- Adaptable to Changes and New Systems – Robotic systems can change over time due to wear, damage, or other alterations. Data-driven approaches can be used to continuously or periodically update the system mode. Moreover, this can be applied to various robotic systems without needing in-depth knowledge of each system’s unique physics. This makes it a versatile tool for researchers or engineers working with multiple robotic platforms.

The model of this car before (left) and after (right) would be much different due to the significant wear and tear. Data-driven models are easier to update continuously throughout the life of a system.
Disadvantages of Data-Driven System Identification
While data-driven system identification offers many advantages, it’s essential to understand its limitations too. For instance, it requires adequate data quality and quantity. Overfitting can be a concern if the data is not representative of the system’s operational range. Moreover, a purely data-driven model might lack the interpretability that physics-based models offer.
- Interpretability – Data-driven models, especially complex ones like neural networks, can act as “black boxes,” meaning that while they might be accurate, they do not provide intuitive insights into the underlying physical processes. This can be problematic in scenarios where understanding the underlying dynamics is crucial.
- Extrapolation – If a robotic system is identified under a particular set of conditions (e.g., a specific temperature or type of terrain), the model might not perform well when those conditions change, unless those changes were included in the training data.
- Computational Overhead – Some data-driven techniques, particularly sophisticated machine learning algorithms, require significant computational resources for both training and inference.
- Lack of Physical Constraints – Purely data-driven models might produce results that violate known physical laws or constraints unless these are explicitly incorporated into the modeling process.
The Elegance of a Hybrid Approach
A hybrid approach, combining the strengths of dynamics-based (or physics-based) and data-driven modeling, can be used to minimize the disadvantages of black-box approaches. Here at 3Laws, our typical modeling framework involves a two-pronged approach of a dynamics model and neural network component.
The key component of a hybrid approach is to calibrate the correct resolution of the model and the size of the neural network that best fits our compute budget and performance requirements. We are trying to balance the fundamental tradeoff between model accuracy and compute time.
1. Dynamical Model Based Component
The strategy is to build the simplest most computationally efficient model that, when paired with a neural network, produces the desired accuracy within the compute budget. They keys are:
- Use straightforward system identification with a simplified model. This typically involves optimizing over parameters in an ODE representation of the dynamics. This could be, for example, solving for time constants in a kinematic model of a vehicle.
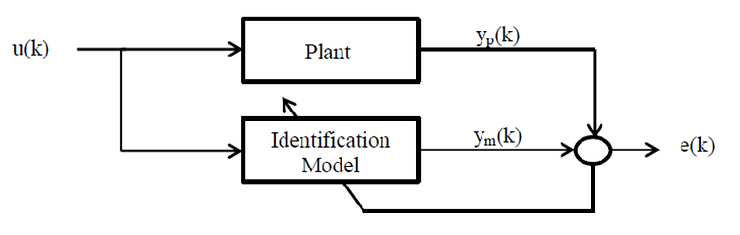
Typical System Identification Block Model
- Integrate additional modeling components that have proven essential or are known to be well-understood and parameterized. This could be, for example, adding a rich engine powertrain model with uncertain parameters.
- Make a suite of unit tests with cases that are representative of your nominal environment, as well as known edge-cases.
2. Neural Network Component
We train a black box model on the pre-processed data and evaluate its performance. This is mostly to evaluate the correct model size for the compute budget rather than accuracy.
- Once we do this we will attempt to pair the neural network with one of the model-based components. We will explore several alternatives for this purpose:
- A neural network trained to learn the residual error of the dynamics-based model.
- Learn residuals of individual components of the high-fidelity model with high error.
- Finally we will attempt to provide estimates of the model uncertainty in different regions of the state-space. This step is only necessary if we still observe significant model mismatch in regions of the state-space.
Navigating the Complexity of Robotic Systems Through a Hybrid Approach
In the rapidly evolving world of robotics, finding an optimal solution for system identification is an ongoing challenge. Data-driven system identification provides a robust mechanism for creating dynamic models, with significant benefits such as increased accuracy, adaptability to changes, and reduced modeling efforts. However, there are also real limitations: limited interpretability and extrapolation, computational overhead, and physical constraints.
The elegance of a hybrid approach, mixing classical physics-based modeling with modern data-driven techniques, emerges as a solution that leverages the strengths of both worlds. At 3Laws, our fusion of dynamics and neural network components aims to balance model accuracy and computational efficiency, presenting an effective way to navigate the complex and multifaceted nature of robotic systems.
The success of this approach underlines the importance of continuous innovation and flexibility in tackling the challenges and unlocking the potential of next-generation robotics.
Further Reading
To see more about our data-driven approach to modeling ODEs, see here, here and here.
To see how we incorporate the learning into the safety-critical control framework, you can get a taste here.
Keep your eyes peeled for a future case study on these methods applied to a real-world system!